Jana Dienstbier, Frauke Liers, Jan Rolfes
https://arxiv.org/abs/2301.11185
In this work, we present algorithmically tractable safe approximations of distributionally robust optimization (DRO) problems. The considered ambiguity sets can exploit information on moments as well as confidence sets. Typically, reformulation approaches using duality theory need to make strong assumptions on the structure of the underlying constraints, such as convexity in the decisions or concavity in the uncertainty. In contrast, here we present a duality-based reformulation approach for DRO problems, where the objective of the adverserial is allowed to depend on univariate indicator functions. This renders the problem nonlinear and nonconvex. In order to be able to reformulate the semiinfinite constraints nevertheless, an exact reformulation is presented that is approximated by a discretized counterpart. The approximation is realized as a mixed-integer linear problem that yields sufficient conditions for distributional robustness of the original problem. Furthermore, it is proven that with increasingly fine discretizations, the discretized reformulation converges to the original distributionally robust problem. The approach is made concrete for a challenging, fundamental task in particle separation that appears in material design. Computational results for realistic settings show that the safe approximation yields robust solutions of high-quality and can be computed within short time.
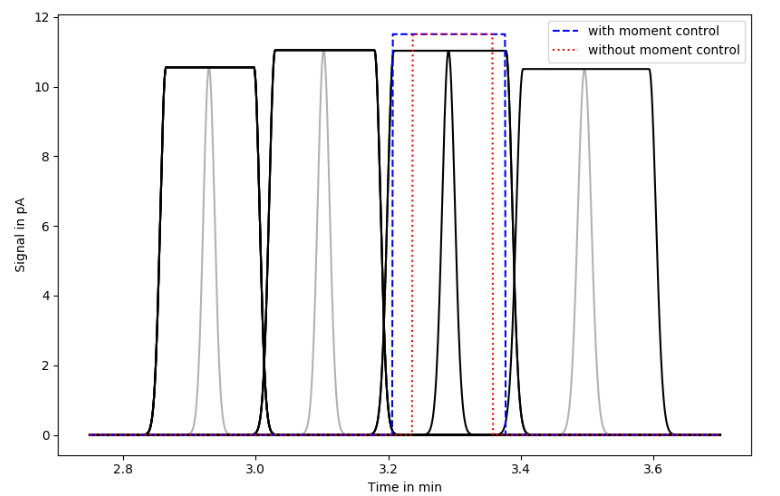
Jana Dienstbier, Frauke Liers, Jan Rolfes
https://arxiv.org/abs/2301.11185
In this work, we present algorithmically tractable safe approximations of distributionally robust optimization (DRO) problems. The considered ambiguity sets can exploit information on moments as well as confidence sets. Typically, reformulation approaches using duality theory need to make strong assumptions on the structure of the underlying constraints, such as convexity in the decisions or concavity in the uncertainty. In contrast, here we present a duality-based reformulation approach for DRO problems, where the objective of the adverserial is allowed to depend on univariate indicator functions. This renders the problem nonlinear and nonconvex. In order to be able to reformulate the semiinfinite constraints nevertheless, an exact reformulation is presented that is approximated by a discretized counterpart. The approximation is realized as a mixed-integer linear problem that yields sufficient conditions for distributional robustness of the original problem. Furthermore, it is proven that with increasingly fine discretizations, the discretized reformulation converges to the original distributionally robust problem. The approach is made concrete for a challenging, fundamental task in particle separation that appears in material design. Computational results for realistic settings show that the safe approximation yields robust solutions of high-quality and can be computed within short time.