Jana Dienstbier, Frauke Liers, Jan Rolfes
https://arxiv.org/abs/2310.05612
Single-level reformulations of (non-convex) distributionally robust optimization (DRO) problems are often intractable, as they contain semiinfinite dual constraints. Based on such a semiinfinite reformulation, we present a safe approximation, that allows for the computation of feasible solutions for DROs that depend on nonconvex multivariate simple functions. Moreover, the approximation allows to address ambiguity sets that can incorporate information on moments as well as confidence sets. The typical strong assumptions on the structure of the underlying constraints, such as convexity in the decisions or concavity in the uncertainty found in the literature were, at least in part, recently overcome in [9]. We start from the duality-based reformulation approach in [9] that can be applied for DRO constraints based on simple functions that are univariate in the uncertainty parameters. We significantly extend their approach to multivariate simple functions which leads to a considerably wider applicability of the proposed reformulation approach. In order to achieve algorithmic tractability, the presented safe approximation is then realized by a discretized counterpart for the semiinfinite dual constraints. The approximation leads to a computationally tractable mixed-integer positive semidefinite problem for which state-of-the-art software implementations are readily available. The tractable safe approximation provides sufficient conditions for distributional robustness of the original problem, i.e., obtained solutions are provably robust.
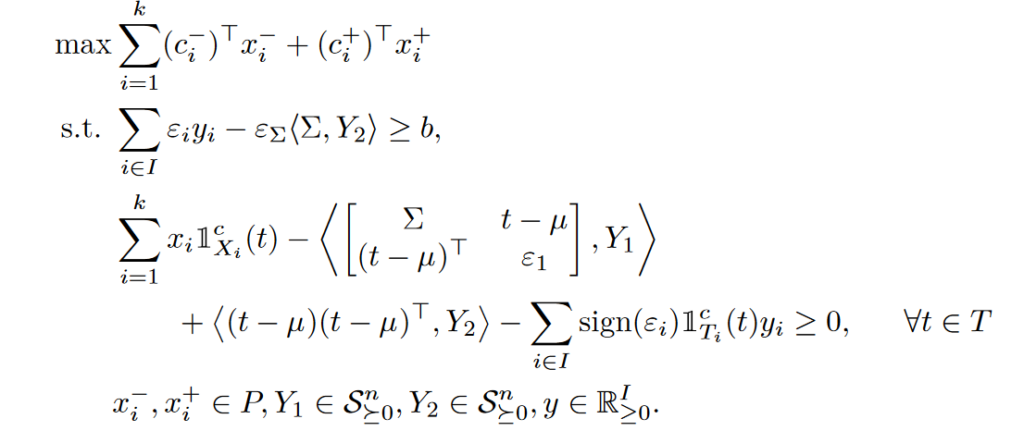
Jana Dienstbier, Frauke Liers, Jan Rolfes
https://arxiv.org/abs/2310.05612
Single-level reformulations of (non-convex) distributionally robust optimization (DRO) problems are often intractable, as they contain semiinfinite dual constraints. Based on such a semiinfinite reformulation, we present a safe approximation, that allows for the computation of feasible solutions for DROs that depend on nonconvex multivariate simple functions. Moreover, the approximation allows to address ambiguity sets that can incorporate information on moments as well as confidence sets. The typical strong assumptions on the structure of the underlying constraints, such as convexity in the decisions or concavity in the uncertainty found in the literature were, at least in part, recently overcome in [9]. We start from the duality-based reformulation approach in [9] that can be applied for DRO constraints based on simple functions that are univariate in the uncertainty parameters. We significantly extend their approach to multivariate simple functions which leads to a considerably wider applicability of the proposed reformulation approach. In order to achieve algorithmic tractability, the presented safe approximation is then realized by a discretized counterpart for the semiinfinite dual constraints. The approximation leads to a computationally tractable mixed-integer positive semidefinite problem for which state-of-the-art software implementations are readily available. The tractable safe approximation provides sufficient conditions for distributional robustness of the original problem, i.e., obtained solutions are provably robust.